ベイズ勉強会 Part 4 多次元ガウス分布のベイズ推論
多次元ガウス分布のベイズ推論を実践する
ベイズ勉強会資料は『ベイズ推論による機械学習入門』1を元に、途中式計算をできるだけ省略せずに行ったものです。
Important: 多次元ガウス分布の確率密度関数 $$\frac{1}{\sqrt{(2\pi)^D |{\bf \Sigma} }|}\exp{\{-\frac{1}{2}({\bf x}-{\bf \mu})^\mathrm{T} {\bf \Sigma}^{-1} ({\bf x}-{\bf \mu})\} }$$
${\bf \mu} \in \mathbb{R}^D$は平均パラメータ、${\bf \Sigma}$は共分散行列パラメータで$D \times D$の正定値行列である必要がある。
Important: 正定値行列
固有値が全て正の実正方行列を正定値行列と呼ぶ。実正方行列${\bf A}$が正定値行列である必要十分条件は任意の非ゼロベクトル${\bf x}$に関して、
$${\bf x}^\mathrm{T} {\bf A}{\bf x} > 0$$が成り立つこと。正定値行列の逆行列も正定値行列である。また全ての固有値が正であることから、
$$|{\bf A}| > 0$$が成り立つ。
また、対称行列であるので
$${\bf A}^{\mathrm{T} } = {\bf A}$$が成り立つ。
多次元ガウス分布を対数で表示すると、
Important: 多次元ガウス分布の対数表示 $$\ln \mathcal{N}({\bf x}|{\bf \mu},{\bf \Sigma})=-\frac{1}{2}\{({\bf x}-{\bf \mu})^\mathrm{T} {\bf \Sigma}^{-1}({\bf x}-{\bf \mu}) + \ln |{\bf \Sigma}| + D \ln 2\pi\}$$
1次元ガウス分布と同様に分散の逆元として精度を定義できる。共分散行列$\bf{\Sigma}$の逆行列として精度行列$\bf{\Lambda}$を定義する。すなわち$\bf{\Lambda}=\bf{\Sigma}^{-1}$である。
Important: 多次元ガウス分布を精度行列で表した場合 $$\frac{1}{\sqrt{(2\pi)^D} }|{\bf \Lambda}|^{\frac{1}{2} }\exp{\{-\frac{1}{2}({\bf x}-{\bf \mu})^\mathrm{T} {\bf \Lambda} ({\bf x}-{\bf \mu})\} }$$
Important: 多次元ガウス分布の対数表示(精度行列で表した場合) $$\ln \mathcal{N}({\bf x}|{\bf \mu},{\bf \Lambda}^{-1})=-\frac{1}{2}\{({\bf x}-{\bf \mu})^\mathrm{T} {\bf \Lambda}({\bf x}-{\bf \mu}) - \ln |{\bf \Lambda}| + D\ln 2\pi\}$$
この多次元ガウス分布のベイズ推論を行っていく。1次元ガウス分布と同様、平均パラメータ未知、精度パラメータ未知、両方未知の場合の順に行う。なお本稿では特に断り無い限り多次元ガウス分布のことをガウス分布と呼ぶ。
平均未知
D次元の確率変数${\bf x} \in \mathbb{R}^D$の平均パラメータ${\bf \mu} \in \mathbb{R}^D$のみが未知で、精度行列${\bf \Lambda} \in \mathbb{R}^{D \times D}$は既に与えられている、またはハイパーパラメータとして、ベイズ推論を行ってみる。N個のデータ${\bf X} = \{ {\bf x}_1,\dots,{\bf x}_N\}$が観測されていて、予測する未知の観測を${\bf x}_*$とおく。
モデルの構築
平均のみが未知の時は、ガウス分布を事前分布とすることで共役性が満たされることがわかっている。${\bf m} \in \mathbb{R}^D, {\bf \Lambda}_{\mu} \in \mathbb{R}^{D \times D}$をハイパーパラメータとして同時分布は次のようになる。
$$ \begin{eqnarray} p({\bf X},{\bf x}_*,{\bf \mu}) &=& p({\bf X}|{\bf \mu})p({\bf x}_*|{\bf \mu})p({\bf \mu}) \\ p({\bf X}|{\bf \mu}) &=& \Pi_{n=1}^{N} \mathcal{N}({\bf x}_n|{\bf \mu},{\bf \Lambda}^{-1}) \\ p({\bf x}_*|{\bf \mu}) &=& \mathcal{N}({\bf x}_*|{\bf \mu},{\bf \Lambda}^{-1}) \\ p({\bf \mu}) &=& \mathcal{N}({\bf \mu}|{\bf m},{\bf \Lambda}_{\mu}^{-1}) \end{eqnarray} $$事後分布の推論
ベイズの定理を用いて事後分布$p({\bf \mu}|{\bf X})$は次のようになる。
$$ \begin{eqnarray} p({\bf \mu}|{\bf X}) &\propto& p({\bf X}|{\bf \mu})p({\bf \mu}) \\ &=& \{ \Pi_{n=1}^{N} p({\bf x}_n|{\bf \mu})\}p({\bf \mu}) \\ &=& \Pi_{n=1}^{N} \{\mathcal{N}({\bf x}_n|{\bf \mu},{\bf \Lambda}^{-1})\} \mathcal{N}({\bf \mu}|{\bf m},{\bf \Lambda}_{\mu}^{-1}) \end{eqnarray} $$対数をとると
$$ \begin{eqnarray} \ln p({\bf \mu}|{\bf X}) &=& \Sigma_{n=1}^{N} \ln \mathcal{N}({\bf x}_n|{\bf \mu},{\bf \Lambda}^{-1}) + \ln \mathcal{N}({\bf \mu}|{\bf m},{\bf \Lambda}_{\mu}^{-1}) + const. \\ &=& -\frac{1}{2} \Sigma_{n=1}^{N} ({\bf x}_n-{\bf \mu})^\mathrm{T} {\bf \Lambda}({\bf x}_n-{\bf \mu}) - \frac{1}{2}({\bf \mu}-{\bf m})^\mathrm{T}{\bf \Lambda}_{\mu}({\bf \mu}-{\bf m}) + const. \\ &=& -\frac{1}{2} \Sigma_{n=1}^{N} ({\bf x}_n^{\mathrm{T} }-{\bf \mu}^{\mathrm{T} }){\bf \Lambda}({\bf x}_n-{\bf \mu}) - \frac{1}{2}({\bf \mu}^{\mathrm{T} }-{\bf m}^{\mathrm{T} }) {\bf \Lambda}_{\mu}({\bf \mu}-{\bf m}) + const. \\ &=& \frac{1}{2}\Sigma_{n=1}^{N}\{ {\bf x}_n^{\mathrm{T} }{\bf \Lambda}{\bf \mu}\} + \frac{1}{2} {\bf \mu}^{\mathrm{T} } {\bf \Lambda}\Sigma_{n=1}^{N} {\bf x}_n - \frac{N}{2} {\bf \mu}^{\mathrm{T} }{\bf \Lambda}{\bf \mu} - \frac{1}{2} {\bf \mu}^{\mathrm{T} }{\bf \Lambda}_{\mu}{\bf \mu} + \frac{1}{2}{\bf \mu}^{\mathrm{T} }{\bf \Lambda}_{\mu}{\bf m} + \frac{1}{2}{\bf m}^{\mathrm{T} }{\bf \Lambda}_{\mu}{\bf \mu} + const. \end{eqnarray} $$ここで、${\bf x}_n^{\mathrm{T} }{\bf \Lambda}{\bf \mu}$は行数と列数について(1×D)×(D×D)×(D×1)=(1×1)よりスカラーなので次が成り立つ。
$$ \begin{eqnarray} {\bf x}_n^{\mathrm{T} }{\bf \Lambda}{\bf \mu} &=& ({\bf x}_n^{\mathrm{T} }{\bf \Lambda}{\bf \mu})^{\mathrm{T} } (スカラーを転置しても同じ) \\ &=& {\bf \mu}^{\mathrm{T} } {\bf \Lambda}^{\mathrm{T} } {\bf x}_n (これは公式通り) \\ &=& {\bf \mu}^{\mathrm{T} } {\bf \Lambda} {\bf x}_n ({\bf \Lambda}は対称行列) \end{eqnarray} $$${\bf m}^{\mathrm{T} }{\bf \Lambda}_{\mu} {\bf \mu}$についても同様であり、
$$ \begin{eqnarray} \ln p({\bf \mu}|{\bf X}) &=& \frac{1}{2}\Sigma_{n=1}^{N}\{ {\bf x}_n^{\mathrm{T} }{\bf \Lambda}{\bf \mu}\} + \frac{1}{2} {\bf \mu}^{\mathrm{T} } {\bf \Lambda}\Sigma_{n=1}^{N} {\bf x}_n - \frac{N}{2} {\bf \mu}^{\mathrm{T} }{\bf \Lambda}{\bf \mu} - \frac{1}{2} {\bf \mu}^{\mathrm{T} }{\bf \Lambda}_{\mu}{\bf \mu} + \frac{1}{2}{\bf \mu}^{\mathrm{T} }{\bf \Lambda}_{\mu}{\bf m} + \frac{1}{2}{\bf m}^{\mathrm{T} }{\bf \Lambda}_{\mu}{\bf \mu} + const. \\ &=& \frac{1}{2}{\bf \mu}^{\mathrm{T} } {\bf \Lambda}\Sigma_{n=1}^{N} {\bf x}_n + \frac{1}{2}{\bf \mu}^{\mathrm{T} } {\bf \Lambda}\Sigma_{n=1}^{N} {\bf x}_n - \frac{N}{2} {\bf \mu}^{\mathrm{T} }{\bf \Lambda}{\bf \mu} - \frac{1}{2} {\bf \mu}^{\mathrm{T} }{\bf \Lambda}_{\mu}{\bf \mu} + \frac{1}{2}{\bf \mu}^{\mathrm{T} }{\bf \Lambda}_{\mu}{\bf m} + + \frac{1}{2}{\bf \mu}^{\mathrm{T} }{\bf \Lambda}_{\mu}{\bf m} + const. \\ &=& - \frac{1}{2}\{ {\bf \mu}^{\mathrm{T} } (N {\bf \Lambda}+{\bf \Lambda}_{\mu}){\bf \mu} - 2 {\bf \mu}^{\mathrm{T} }({\bf \Lambda} \Sigma_{n=1}^{N} {\bf x}_n + {\bf \Lambda}_{\mu} {\bf m})\} + const. \end{eqnarray} $$${\bf \mu}$に関する上に凸の二次関数となり、ガウス分布であることがわかる。1次元と同様に逆算的に計算していく。
$$p({\bf \mu}|{\bf X}) = \mathcal{N}({\bf \mu}|\hat{\bf m},\hat{\bf \Lambda}_{\bf \mu}^{-1})$$
とおき、対数をとって${\bf \mu}$について整理すると
$$ \begin{eqnarray} \ln p({\bf \mu}|{\bf X}) &=& -\frac{1}{2}\{({\bf \mu}-\hat{\bf m})^\mathrm{T} \hat{\bf \Lambda}_{\bf \mu} ({\bf \mu}-\hat{\bf m}) \} + const. \\ &=& -\frac{1}{2} \{ {\bf \mu}^{\mathrm{T} } \hat{\bf \Lambda}_{\bf \mu} {\bf \mu} - \hat{\bf m}^{\mathrm{T} } \hat{\bf \Lambda}_{\bf \mu} {\bf \mu} - {\bf \mu}^{\mathrm{T} } \hat{\bf \Lambda}_{\bf \mu} \hat{\bf m} \} + const. \\ &=& -\frac{1}{2} \{ {\bf \mu}^{\mathrm{T} } \hat{\bf \Lambda}_{\bf \mu} {\bf \mu}-2{\bf \mu}^{\mathrm{T} } \hat{\bf \Lambda}_{\bf \mu} \hat{\bf m} \} + const. \end{eqnarray} $$対応関係を見れば
$$ \begin{eqnarray} \hat{\bf \Lambda}_{\bf \mu} = N{\bf \Lambda}+{\bf \Lambda}_{\bf \mu} \\ \hat{\bf m} = \hat{\bf \Lambda}_{\bf \mu}^{-1}({\bf \Lambda} \Sigma_{n=1}^{N} {\bf x}_n + {\bf \Lambda}_{\mu} {\bf m}) \end{eqnarray} $$と事後分布のハイパーパラメータが求まる。
予測分布の導出
簡単のために学習前の事前分布を用いて予測分布を導出し、更新されたハイパーパラメータを代入することで学習後の予測分布を計算する。1次元の時と同様、ベイズの定理と対数化を利用し積分計算を避ける。
$$\ln p({\bf x}_*) = \ln p({\bf x}_*|{\bf \mu}) - \ln p({\bf \mu}|{\bf x}_*) + const.$$
$\ln p({\bf \mu}|{\bf x}_*)$は${\bf x}_*$を学習した後の事後分布と見なせるので、
$$ \begin{eqnarray} p({\bf \mu}|{\bf x}_*) &=& \mathcal{N}({\bf \mu}|{\bf m}({\bf x}_*), ({\bf \Lambda}+{\bf \Lambda}_{\bf \mu})^{-1}) \\ ただし {\bf m}({\bf x}_*) &=& ({\bf \Lambda}+{\bf \Lambda}_{\bf \mu})^{-1} ({\bf \Lambda}{\bf x}_* + {\bf \Lambda}_{\bf \mu} {\bf m}) \end{eqnarray} $$したがって、
$$ \begin{eqnarray} \ln p({\bf x}_*) &=& \ln p({\bf x}_*|{\bf \mu}) - \ln p({\bf \mu}|{\bf x}_*) + const. \\ &=& -\frac{({\bf x}_*-{\bf \mu})^\mathrm{T}{\bf \Lambda}({\bf x}_*-{\bf \mu})}{2} + \frac{({\bf \mu}-{\bf m}({\bf x}_*))^\mathrm{T}({\bf \Lambda}+{\bf \Lambda}_{\mu})({\bf \mu}-{\bf m}({\bf x}_*))}{2} + const. \\ &=& -\frac{1}{2}\{ {\bf x}_*^{\mathrm{T} }{\bf \Lambda}{\bf x}_* - {\bf x}_*^{\mathrm{T} }{\bf \Lambda}{\bf \mu} - {\bf \mu}^\mathrm{T}{\bf \Lambda}{\bf x}_* - {\bf m}({\bf x}_*)^\mathrm{T} ({\bf \Lambda}+{\bf \Lambda}_{\bf \mu}) {\bf m}({\bf x}_*) + {\bf m}({\bf x}_*)^\mathrm{T}({\bf \Lambda}+{\bf \Lambda}_{\bf \mu}){\bf \mu} + {\bf \mu}^\mathrm{T}({\bf \Lambda}+{\bf \Lambda}_{\bf \mu}){\bf m}({\bf x}_*) \} + const. \\ &=& -\frac{1}{2}\{ {\bf x}_*^{\mathrm{T} }{\bf \Lambda}{\bf x}_* - 2 {\bf x}_*^{\mathrm{T} }{\bf \Lambda}{\bf \mu} - {\bf m}({\bf x}_*)^\mathrm{T} ({\bf \Lambda}+{\bf \Lambda}_{\bf \mu}) {\bf m}({\bf x}_*) + 2 {\bf \mu}^\mathrm{T}({\bf \Lambda}+{\bf \Lambda}_{\bf \mu}){\bf m}({\bf x}_*)\} + const. \\ &=& -\frac{1}{2}\{ {\bf x}_*^{\mathrm{T} }{\bf \Lambda}{\bf x}_* - 2 {\bf x}_*^{\mathrm{T} }{\bf \Lambda}{\bf \mu} - {\bf m}({\bf x}_*)^\mathrm{T} ({\bf \Lambda}{\bf x}_* + {\bf \Lambda}_{\bf \mu}{\bf m}) + 2{\bf \mu}^\mathrm{T}{\bf \Lambda}{\bf x}_*\} + const. \\ &=& -\frac{1}{2}\{ {\bf x}_*^{\mathrm{T} }{\bf \Lambda}{\bf x}_* - ({\bf \Lambda}{\bf x}_* + {\bf \Lambda}_{\bf \mu}{\bf m})^\mathrm{T} {\bf m}({\bf x}_*) \} + const. ({\bf m}({\bf x}_*)^\mathrm{T} ({\bf \Lambda}{\bf x}_* + {\bf \Lambda}_{\bf \mu}{\bf m})はスカラーなので転置しても変わらない) \\ &=& -\frac{1}{2}\{ {\bf x}_*^{\mathrm{T} }{\bf \Lambda}{\bf x}_* - ({\bf \Lambda}{\bf x}_* + {\bf \Lambda}_{\bf \mu}{\bf m})^\mathrm{T} ({\bf \Lambda}+{\bf \Lambda}_{\bf \mu})^{-1} ({\bf \Lambda}{\bf x}_* + {\bf \Lambda}_{\bf \mu}{\bf m}) \} + const. \\ &=& -\frac{1}{2}\{ {\bf x}_*^{\mathrm{T} }{\bf \Lambda}{\bf x}_* - ({\bf \Lambda}{\bf x}_*)^\mathrm{T}({\bf \Lambda}+{\bf \Lambda}_{\bf \mu})^{-1}{\bf \Lambda}{\bf x}_* - ({\bf \Lambda}{\bf x}_*)^\mathrm{T}({\bf \Lambda}+{\bf \Lambda}_{\bf \mu})^{-1}{\bf \Lambda}_{\bf \mu}{\bf m} - ({\bf \Lambda}_{\bf \mu}{\bf m})^\mathrm{T}({\bf \Lambda}+{\bf \Lambda}_{\bf \mu})^{-1}{\bf \Lambda}{\bf x}_*\} + const. \\ &=& -\frac{1}{2}\{ {\bf x}_*^{\mathrm{T} }{\bf \Lambda}{\bf x}_* - {\bf x}_*^\mathrm{T}{\bf \Lambda}({\bf \Lambda}+{\bf \Lambda}_{\bf \mu})^{-1}{\bf \Lambda}{\bf x}_* - 2{\bf x}_*^\mathrm{T}{\bf \Lambda}({\bf \Lambda}+{\bf \Lambda}_{\bf \mu})^{-1}{\bf \Lambda}_{\bf \mu}{\bf m} \} + const. \\ &=& -\frac{1}{2}\{ {\bf x}_*^{\mathrm{T} } ({\bf \Lambda}-{\bf \Lambda}({\bf \Lambda}+{\bf \Lambda}_{\bf \mu})^{-1}{\bf \Lambda}) {\bf x}_* - 2{\bf x}_*^\mathrm{T}{\bf \Lambda}({\bf \Lambda}+{\bf \Lambda}_{\bf \mu})^{-1}{\bf \Lambda}_{\bf \mu}{\bf m} \} + const. \end{eqnarray} $$ここで
$$ p({\bf x}_*) = \mathcal{N}({\bf x}_*|{\bf \mu}_*,{\bf \Lambda}_*^{-1}) $$と書けるとすると
$$ \ln p({\bf x}_*) = -\frac{1}{2} \{ {\bf x}_*^{\mathrm{T} } {\bf \Lambda}_{*} {\bf x}_* -2{\bf x}_*^{\mathrm{T} } {\bf \Lambda}_{*} {\bf \mu}_*\} + const. $$であるから、対応関係から
$$ \begin{eqnarray} {\bf \Lambda}_* &=& {\bf \Lambda}-{\bf \Lambda}({\bf \Lambda}+{\bf \Lambda}_{\bf \mu})^{-1}{\bf \Lambda} \\ {\bf \mu}_* &=& {\bf \Lambda}_*^{-1} {\bf \Lambda}({\bf \Lambda}+{\bf \Lambda}_{\bf \mu})^{-1}{\bf \Lambda}_{\bf \mu}{\bf m} \end{eqnarray} $$ウッドベリーの公式を使うことで更に簡潔な形にできる。
Tip: ウッドベリーの公式 $$({\bf A}+{\bf U}{\bf B}{\bf V})^{-1} = {\bf A}^{-1} - {\bf A}^{-1}{\bf U}({\bf B}^{-1}+{\bf V}{\bf A}^{-1}{\bf U})^{-1}{\bf V}{\bf A}^{-1}$$
Tip: ウッドベリーの公式(${\bf A},{\bf B}$の次元が等しく, ${\bf U},{\bf V}$が単位行列の場合) $$({\bf A}+{\bf B})^{-1} = {\bf A}^{-1} - {\bf A}^{-1}({\bf A}^{-1} + {\bf B}^{-1})^{-1} {\bf A}^{-1}$$
${\bf \Lambda}_*$について、${\bf A}={\bf \Lambda}^{-1},{\bf B}={\bf \Lambda}_{\bf \mu}^{-1}$とおくと、
$$ \begin{eqnarray} {\bf \Lambda}_* &=& {\bf \Lambda}-{\bf \Lambda}({\bf \Lambda}+{\bf \Lambda}_{\bf \mu})^{-1}{\bf \Lambda} \\ &=& {\bf A}^{-1} - {\bf A}^{-1}({\bf A}^{-1} + {\bf B}^{-1})^{-1} {\bf A}^{-1} \\ &=& ({\bf A}+{\bf B})^{-1} \\ &=& ({\bf \Lambda}^{-1} + {\bf \Lambda}_{\mu}^{-1})^{-1} \end{eqnarray} $$${\bf \mu}_*$は、${\bf \Lambda}_* = {\bf \Lambda}-{\bf \Lambda} ({\bf \Lambda}+{\bf \Lambda}_{\bf \mu})^{-1} {\bf \Lambda}$より
$$ \begin{eqnarray} {\bf \Lambda}({\bf \Lambda}+{\bf \Lambda}_{\bf \mu})^{-1}{\bf \Lambda} &=& {\bf \Lambda} - {\bf \Lambda}_* \\ {\bf \Lambda}({\bf \Lambda}+{\bf \Lambda}_{\bf \mu})^{-1} &=& ({\bf \Lambda} - {\bf \Lambda}_*){\bf \Lambda}^{-1} \end{eqnarray} $$だから
$$ \begin{eqnarray} {\bf \mu}_* &=& {\bf \Lambda}_*^{-1} {\bf \Lambda}({\bf \Lambda}+{\bf \Lambda}_{\bf \mu})^{-1}{\bf \Lambda}_{\bf \mu}{\bf m} \\ &=& {\bf \Lambda}_*^{-1} ({\bf \Lambda} - {\bf \Lambda}_*){\bf \Lambda}^{-1}{\bf \Lambda}_{\bf \mu}{\bf m} \\ &=& \{ {\bf \Lambda}_*^{-1}{\bf \Lambda}{\bf \Lambda}^{-1}{\bf \Lambda}_{\bf \mu} - {\bf \Lambda}_*^{-1}{\bf \Lambda}_* {\bf \Lambda}^{-1}{\bf \Lambda}_{\bf \mu} \}{\bf m} \\ &=& \{ {\bf \Lambda}_*^{-1}{\bf \Lambda}_{\bf \mu} - {\bf \Lambda}^{-1}{\bf \Lambda}_{\bf \mu} \}{\bf m} \\ &=& \{ ({\bf \Lambda}^{-1} + {\bf \Lambda}_{\mu}^{-1}){\bf \Lambda}_{\bf \mu} - {\bf \Lambda}^{-1}{\bf \Lambda}_{\bf \mu}\}{\bf m} \\ &=& {\bf I}_D {\bf m} = {\bf m} \end{eqnarray} $$まとめると、
$$ \begin{eqnarray} {\bf \Lambda}_* &=& ({\bf \Lambda}^{-1} + {\bf \Lambda}_{\mu}^{-1})^{-1} \\ {\bf \mu}_* &=& {\bf m} \end{eqnarray} $$これらに、更新されたハイパーパラメータ$\hat{\bf m},\hat{\bf \Lambda}_{\bf \mu}$を代入して学習後の予測分布$p({\bf x}_*|{\bf X})$が求まる。
Important: ウィシャート分布の確率密度関数 $$\mathcal{W}({\bf \Lambda}|\nu,{\bf W}) = C_\mathcal{W} (\nu, {\bf W})|{\bf \Lambda}|^{\frac{\nu-D-1}{2} } exp\{ -\frac{1}{2} Tr({\bf W}^{-1} {\bf \Lambda})\}$$
$\nu$は自由度パラメータで、$\nu > D - 1$を満たす必要がある。また、パラメータ${\bf W}$は$D \times D$の正定値行列である。$Tr()$はトレースといい、行列の対角成分の和をとる演算である。ウィシャート分布も対数化することで計算の見通しが良くなる。
Important: ウィシャート分布の対数化 $$\ln \mathcal{W} ({\bf \Lambda}|\nu,{\bf W}) = \frac{\nu-D-1}{2} \ln |{\bf \Lambda}| - \frac{1}{2} Tr({\bf W}^{-1} {\bf \Lambda}) + \ln C_\mathcal{W} (\nu, {\bf W})$$
Important: 対数化された正規化項 $$\ln C_\mathcal{W} (\nu, {\bf W}) = - \frac{\nu}{2} \ln |{\bf W}| - \ln \frac{\nu D}{2} \ln 2 - \frac{D(D-1)}{4} \ln \pi - \Sigma_{d=1}^{D} \ln \Gamma(\frac{\nu+1+d}{2})$$
Tip: トレースについて成り立つ等式 $$\begin{eqnarray} Tr({\bf A}) &=& Tr({\bf A}^\mathrm{T}) \\ Tr({\bf A} + {\bf B}) &=& Tr({\bf A}) + Tr({\bf B}) \\ Tr({\bf AB}) &=& Tr({\bf BA}) \end{eqnarray}$$
さて、このウィシャート分布を用いてモデルを構築すると次のようになる。
$$ \begin{eqnarray} p({\bf X},{\bf x}_*,{\bf \Lambda}) &=& p({\bf X}|{\bf \Lambda})p({\bf x}_*|{\bf \Lambda})p({\bf \Lambda}) \\ p({\bf x}_*|{\bf \Lambda}) &=& \mathcal{N}({\bf x}_* |{\bf \mu}, {\bf \Lambda}^{-1}) \\ p({\bf X}|{\bf \Lambda}) &=& \Pi_{n=1}^{N} \mathcal{N}({\bf x}_n |{\bf \mu}, {\bf \Lambda}^{-1}) \\ p({\bf \Lambda}) &=& \mathcal{W}({\bf \Lambda}|\nu, {\bf W}) \end{eqnarray} $$事後分布の推論
データ${\bf X}$を観測した後の事後分布は
$$ p({\bf \Lambda}|{\bf X}) \propto p({\bf X}|{\bf \Lambda}) p({\bf \Lambda}) $$ゆえ対数化すると
$$ \begin{eqnarray} \ln p({\bf \Lambda}|{\bf X}) &=& \Sigma_{n=1}^{N} \ln \mathcal{N} ({\bf x}_n|{\bf \mu}, {\bf \Lambda}^{-1}) + \ln \mathcal{W}({\bf \Lambda} |\nu, {\bf W}) + const. \\ &=& - \frac{1}{2} \{ \Sigma_{n=1}^{N} ({\bf x}_n-{\bf \mu})^\mathrm{T} {\bf \Lambda}({\bf x}_n-{\bf \mu}) - N \ln |{\bf \Lambda}| \} + \frac{\nu-D-1}{2} \ln |{\bf \Lambda}| - \frac{1}{2} Tr({\bf W}^{-1} {\bf \Lambda}) + const. \\ &=& \frac{N+\nu-D-1}{2} \ln |{\bf \Lambda}| - \frac{1}{2} \Sigma_{n=1}^{N} Tr \{ ({\bf x}_n-{\bf \mu})^\mathrm{T} {\bf \Lambda}({\bf x}_n-{\bf \mu}) \} - \frac{1}{2} Tr({\bf W}^{-1} {\bf \Lambda}) + const. (スカラーのトレースをとっても同じ) \\ &=& \frac{N+\nu-D-1}{2} \ln |{\bf \Lambda}| - \frac{1}{2} \Sigma_{n=1}^{N} Tr \{ ({\bf x}_n-{\bf \mu})({\bf x}_n-{\bf \mu})^\mathrm{T} {\bf \Lambda} \} - \frac{1}{2} Tr({\bf W}^{-1} {\bf \Lambda}) + const. (トレース内では対角成分が同じであれば順番を入れ替えても問題ない) \\ &=& \frac{N+\nu-D-1}{2} \ln |{\bf \Lambda}| - \frac{1}{2} Tr \left[ \{ \Sigma_{n=1}^{N} ({\bf x}_n-{\bf \mu})({\bf x}_n-{\bf \mu})^\mathrm{T} + {\bf W}^{-1} \} {\bf \Lambda} \right] + const. (トレースの和は和のトレース) \end{eqnarray} $$ウィシャート分布との対応を見れば、
$$ \begin{eqnarray} p({\bf \Lambda}|{\bf X}) &=& \mathcal{W}({\bf \Lambda}|\hat{\nu}, \hat{\bf W}) \\ ただし \hat{\bf W}^{-1} &=& \Sigma_{n=1}^{N} ({\bf x}_n - {\bf \mu})({\bf x}_n - {\bf \mu})^\mathrm{T} + {\bf W}^{-1} \\ \hat{\nu} &=& N + \nu \end{eqnarray} $$となる。
予測分布の導出
事前分布と事後分布の形が同じなので、表記がシンプルになるよう学習前のハイパーパラメータで予測分布を計算し、後で代入する。
積分計算を避け、ベイズの定理と対数を利用する。学習前の予測分布$p({\bf x}_*)$は、
$$ \ln p({\bf x}_*) = \ln p({\bf x}_*|{\bf \Lambda}) - \ln p({\bf \Lambda}|{\bf x}_*) + const. $$と表せる。事後分布の結果を流用して
$$ \begin{eqnarray} p({\bf \Lambda}|{\bf x}_*) &=& \mathcal{W}({\bf \Lambda}|1+\nu , {\bf W}({\bf x}_*)) \\ ただし {\bf W} ({\bf x}_*)^{-1} &=& ({\bf x}_* - {\bf \mu})({\bf x}_* - {\bf \mu})^\mathrm{T} + {\bf W}^{-1} \end{eqnarray} $$よって
$$ \begin{eqnarray} \ln p({\bf x}_*) &=& \ln p({\bf x}_*|{\bf \Lambda}) - \ln p({\bf \Lambda}|{\bf x}_*) + const. \\ &=& -\frac{1}{2} \left[ ({\bf x}_* -{\bf \mu})^\mathrm{T} {\bf \Lambda} ({\bf x}_* -{\bf \mu}) - Tr \{ {\bf W}({\bf x}_*)^{-1}{\bf \Lambda} \} - (\nu + 1) \ln |{\bf W} ({\bf x}_*)| \right] + const. \end{eqnarray} $$行列式、トレースの性質を使いながら計算を進める。
Tip: 行列式の性質 $$\begin{eqnarray} |c{\bf A}| &=& c^N |{\bf A}| \\ |{\bf A}^\mathrm{T}| &=& |{\bf A}| \\ |{\bf A}{\bf B}| &=& |{\bf A}| |{\bf B}| \\ |{\bf A}^{-1}| &=& |{\bf A}|^{-1} \\ |{\bf I}_N + {\bf C} {\bf D}^\mathrm{T} | &=& |{\bf I}_M + {\bf C}^\mathrm{T} {\bf D}| (この{\bf C}と{\bf D}はN \times M行列) \end{eqnarray}$$
$$
\begin{eqnarray}
\ln p({\bf x}_*) &=& -\frac{1}{2} \left[ Tr \{ ({\bf x}_* -{\bf \mu})^\mathrm{T} {\bf \Lambda} ({\bf x}_* -{\bf \mu})) \} - Tr \{ ({\bf x}_* - {\bf \mu})({\bf x}_* - {\bf \mu})^\mathrm{T} {\bf \Lambda}) \} + (\nu + 1) \ln |{\bf W} ({\bf x}_*)^{-1}| \right] + const. \\
&=& - \frac{1+\nu}{2} \ln |({\bf x}_* - {\bf \mu})({\bf x}_* - {\bf \mu})^\mathrm{T} + {\bf W}^{-1}| + const. \\
&=& - \frac{1+\nu}{2} \ln |{\bf W}^{-1} \{ {\bf W} ({\bf x}_* - {\bf \mu})({\bf x}_* - {\bf \mu})^\mathrm{T} + {\bf I}_D \}| + const. \\
&=& - \frac{1+\nu}{2} \ln |{\bf W}^{-1}| |{\bf I}_D + {\bf W} ({\bf x}_* - {\bf \mu})({\bf x}_* - {\bf \mu})^\mathrm{T}| + const. \\
&=& - \frac{1+\nu}{2} \ln |{\bf I}_D + {\bf W} ({\bf x}_* - {\bf \mu})({\bf x}_* - {\bf \mu})^\mathrm{T} | + const. \\
&=& - \frac{1+\nu}{2} \ln |{\bf I}_1 + \{ {\bf W} ({\bf x}_* - {\bf \mu}) \}^\mathrm{T} ({\bf x}_* - {\bf \mu}) | + const. (D \times 1行列になっている) \\
&=& - \frac{1+\nu}{2} \ln \{ 1 + ({\bf x}_* - {\bf \mu})^\mathrm{T} {\bf W} ({\bf x}_* - {\bf \mu}) \} + const.
\end{eqnarray}
$$
これは多次元のStudentのt分布になっている。
Important: 多次元のStudentのt分布: $$St({\bf x} | {\bf \mu}_s , {\bf \Lambda}_s , \nu_s) = \frac{\Gamma(\frac{\nu_s + D}{2})}{\Gamma(\frac{\nu_s}{2})} \frac{|{\bf \Lambda}_s|^{\frac{1}{2} } } {(\pi \nu_s)^{\frac{D}{2} }} \left\{ 1 + \frac{1}{\nu_s} ({\bf x} - {\bf \mu}_s)^\mathrm{T} {\bf \Lambda}_s ({\bf x} - {\bf \mu}_s) \right\}^{- \frac{\nu_s + D}{2} }$$
これを対数化して${\bf x}$に関わる項だけ抜き出すと、
$$ \ln St({\bf x} | {\bf \mu}_s , {\bf \Lambda}_s , \nu_s) = - \frac{\nu_s + D}{2} \ln \left\{ 1 + \frac{1}{\nu_s} ({\bf x} - {\bf \mu}_s)^\mathrm{T} {\bf \Lambda}_s ({\bf x} - {\bf \mu}_s) \right\} + const. $$対応を見ると学習前の予測分布$p({\bf x}_*)$は次のように表せる。
$$ \begin{eqnarray} p({\bf x}_*) &=& St({\bf x} | {\bf \mu}_s , {\bf \Lambda}_s , \nu_s) \\ ただし {\bf \mu}_s &=& {\bf \mu} \\ {\bf \Lambda}_s &=& (1-D+\nu){\bf W} \\ \nu_s &=& 1-D+\nu \end{eqnarray} $$学習後の予測分布$p({\bf x}_* | {\bf X})$はこれに更新されたハイパーパラメータを代入することで求まる。
Important: ガウス・ウィシャート分布 $$NW({\bf \mu}, {\bf \Lambda}|{\bf m},\beta,\nu,{\bf W}) = \mathcal{N}({\bf \mu}|{\bf m}, (\beta {\bf \Lambda})^{-1}) \mathcal{W} ({\bf \Lambda}|\nu, {\bf W})$$
ガウス・ウィシャート分布を事前分布とした場合のモデルは次のようになる。
$$ \begin{eqnarray} p({\bf X},{\bf x}_*,{\bf \mu}, {\bf \Lambda}) &=& p({\bf X}|{\bf \mu}, {\bf \Lambda})p({\bf x}_*|{\bf \mu}, {\bf \Lambda}) p({\bf \mu}) p({\bf \Lambda}) \\ p({\bf \mu}, {\bf \Lambda}) &=& NW({\bf \mu}, {\bf \Lambda}|{\bf m},\beta,\nu,{\bf W}) \end{eqnarray} $$事後分布の推論
データ${\bf X}$を観測した後の事後分布を求める。
$$ \begin{eqnarray} p({\bf \mu}, {\bf \Lambda}| {\bf X}) &=& \frac{p({\bf X}, {\bf \mu}, {\bf \Lambda})}{p({\bf X})} \\ &=& \frac{p({\bf \mu}|{\bf \Lambda}, {\bf X}) p({\bf \Lambda}|{\bf X}) p({\bf X}) }{p({\bf X})} \\ &=& p({\bf \mu}|{\bf \Lambda}, {\bf X}) p({\bf \Lambda}|{\bf X}) \end{eqnarray} $$1次元の場合と同様に、平均と精度の事後分布を別々に求めてみる。
平均の事後分布
平均未知の場合の事後分布で精度行列を$\beta {\bf \Lambda}$とおくことにより求まる。
$$ \begin{eqnarray} p({\bf \mu}|{\bf \Lambda}, {\bf X}) &=& \mathcal{N}({\bf \mu}|\hat{\bf m}, (\hat{\beta} {\bf \Lambda})^{-1}) \\ ただし \hat{\beta} &=& N + \beta \\ \hat{\bf m} &=& \frac{1}{\hat{\beta}}(\Sigma_{n=1}^{N} {\bf x}_n + \beta {\bf m}) \end{eqnarray} $$
Note: この部分の式変形 $$\begin{eqnarray} {\bf \Lambda}_{\bf \mu} &=& \beta {\bf \Lambda}, \hat{\bf \Lambda}_{\bf \mu} = \hat{\beta} {\bf \Lambda} とおいて平均未知の式を見れば、 \\ \hat{\beta} {\bf \Lambda} &=& N {\bf \Lambda} + \beta {\bf \Lambda} ゆえ \\ \hat{\beta} &=& N + \beta \\ \hat{\bf m} &=& \frac{1}{\hat{\beta} } \hat{\bf \Lambda}^{-1} ({\bf \Lambda} \Sigma_{n=1}^{N} {\bf x}_n + \beta {\bf \Lambda} {\bf m}) \\ &=& \frac{1}{\hat{\beta} }(\Sigma_{n=1}^{N} {\bf x}_n + \beta {\bf m}) \end{eqnarray}$$
精度の事後分布
ベイズの定理より、
$$ p({\bf \mu}, {\bf \Lambda}| {\bf X}) = \frac{p({\bf X}|{\bf \mu}, {\bf \Lambda})p({\bf \mu},{\bf \Lambda})}{p({\bf X})} $$が成り立つので、
$$ \begin{eqnarray} p({\bf \mu}|{\bf \Lambda}, {\bf X}) p({\bf \Lambda}|{\bf X}) &=& \frac{p({\bf X}|{\bf \mu}, {\bf \Lambda})p({\bf \mu},{\bf \Lambda})}{p({\bf X})} \\ p({\bf \Lambda}|{\bf X}) &=& \frac{p({\bf X}|{\bf \mu}, {\bf \Lambda})p({\bf \mu},{\bf \Lambda})}{p({\bf X})p({\bf \mu}|{\bf \Lambda}, {\bf X})} \\ \ln p({\bf \Lambda}|{\bf X}) &=& \ln p({\bf X}|{\bf \mu}, {\bf \Lambda}) + \ln p({\bf \mu},{\bf \Lambda}) - \ln p({\bf \mu}|{\bf \Lambda}, {\bf X}) + const. \\ &=& \Sigma_{n=1}^{N} \ln \mathcal{N}({\bf x}_n|{\bf \mu}, {\bf \Lambda}^{-1}) + \ln NW({\bf \mu}, {\bf \Lambda}|{\bf m},\beta,\nu,{\bf W}) - \ln \mathcal{N}({\bf \mu}|\hat{\bf m}, (\hat{\beta} {\bf \Lambda})^{-1}) + const. \\ &=& \Sigma_{n=1}^{N} \ln \mathcal{N}({\bf x}_n|{\bf \mu}, {\bf \Lambda}^{-1}) + \ln \mathcal{N}({\bf \mu}|{\bf m}, (\beta {\bf \Lambda})^{-1}) + \ln \mathcal{W} ({\bf \Lambda}|\nu, {\bf W}) - \ln \mathcal{N}({\bf \mu}|\hat{\bf m}, (\hat{\beta} {\bf \Lambda})^{-1}) + const. \\ &=& - \frac{1}{2} \{ \Sigma_{n=1}^{N} ({\bf x}_n - {\bf \mu})^\mathrm{T} {\bf \Lambda} ({\bf x}_n - {\bf \mu}) - N \ln |{\bf \Lambda}| \} - \frac{\beta}{2} ({\bf \mu} - {\bf m})^\mathrm{T} {\bf \Lambda} ({\bf \mu} - {\bf m}) + \frac{1}{2} \ln |\beta {\bf \Lambda}| + \frac{\nu-D-1}{2} \ln |{\bf \Lambda}| - \frac{1}{2} Tr({\bf W}^\mathrm{T} {\bf \Lambda}) + \frac{\hat{\beta}}{2} ({\bf \mu} - \hat{\bf m})^\mathrm{T} {\bf \Lambda} ({\bf \mu} - \hat{\bf m}) - \frac{1}{2} \ln |\hat{\beta} {\bf \Lambda}| + const. \\ &=& - \frac{1}{2} \{ \Sigma_{n=1}^{N} ({\bf x}_n - {\bf \mu})^\mathrm{T} {\bf \Lambda} ({\bf x}_n - {\bf \mu}) - N \ln |{\bf \Lambda}| \} - \frac{\beta}{2} ({\bf \mu} - {\bf m})^\mathrm{T} {\bf \Lambda} ({\bf \mu} - {\bf m}) + \frac{1}{2} \ln |{\bf \Lambda}| + \frac{\nu-D-1}{2} \ln |{\bf \Lambda}| - \frac{1}{2} Tr({\bf W}^{-1} {\bf \Lambda}) + \frac{\hat{\beta}}{2} ({\bf \mu} - \hat{\bf m})^\mathrm{T} {\bf \Lambda} ({\bf \mu} - \hat{\bf m}) - \frac{1}{2} \ln |{\bf \Lambda}| + const. (|\beta {\bf \Lambda}|=\beta^{D} |{\bf \Lambda}|だが対数を取っているのでconst.に吸収させている。) \\ &=& \frac{N+\nu-D-1}{2} \ln |{\bf \Lambda}| - \frac{1}{2} Tr \left[ \{ \Sigma_{n=1}^{N} {\bf x}_n {\bf x}_n^\mathrm{T} + \beta {\bf m} {\bf m}^\mathrm{T} - \hat{\beta} \hat{\bf m} \hat{\bf m}^\mathrm{T} + {\bf W}^{-1} \} {\bf \Lambda} \right] + const. (スカラーはトレースを取ってまとめた) \end{eqnarray} $$と整理できる。これをウィシャート分布の定義式と対応関係を取って
$$ \begin{eqnarray} p({\bf \Lambda}|{\bf X}) &=& \mathcal{W}({\bf \Lambda}|\hat{\nu},\hat{\bf W}) \\ ただし \hat{\bf W}^{-1} &=& \Sigma_{n=1}^{N} {\bf x}_n {\bf x}_n^\mathrm{T} + \beta {\bf m} {\bf m}^\mathrm{T} - \hat{\beta} \hat{\bf m} \hat{\bf m}^\mathrm{T} + {\bf W}^{-1} \\ \hat{\nu} &=& N + \nu \end{eqnarray} $$事後分布をまとめる
以上をまとめて事後分布は次のようになる。
$$ \begin{eqnarray} p({\bf \mu}, {\bf \Lambda}|{\bf X}) &=& NW({\bf \mu}, {\bf \Lambda}| \hat{\bf m}, \hat{\beta}, \hat{\nu}, \hat{\bf W}) \\ ただし \hat{\beta} &=& N + \beta \\ \hat{\bf m} &=& \frac{1}{\hat{\beta}}(\Sigma_{n=1}^{N} {\bf x}_n + \beta {\bf m}) \\ ただし \hat{\bf W}^{-1} &=& \Sigma_{n=1}^{N} {\bf x}_n {\bf x}_n^\mathrm{T} + \beta {\bf m} {\bf m}^\mathrm{T} - \hat{\beta} \hat{\bf m} \hat{\bf m}^\mathrm{T} + {\bf W}^{-1} \\ \hat{\nu} &=& N + \nu \end{eqnarray} $$予測分布の導出
今回も積分による導出を避けベイズの定理と対数で予測分布を導出する。また、記述がシンプルになるので事前分布を用いた予測分布を導出し後で更新されたハイパーパラメータを代入する。
ベイズの定理により、予測分布$p({\bf x}_*)$は次のように表せる。
$$ \ln p({\bf x}_*) = \ln p({\bf x}_*|{\bf \mu}, {\bf \Lambda}) - \ln p({\bf \mu}, {\bf \Lambda}|{\bf x}_*) + const. $$$\ln p({\bf \mu}, {\bf \Lambda}|{\bf x}_*)$は事後分布の計算結果を流用して
$$ \begin{eqnarray} p({\bf \mu}, {\bf \Lambda}|{\bf x}_*) &=& \mathcal{N}({\bf \mu}|{\bf m}({\bf x}_*), ((1+\beta){\bf \Lambda})^{-1}) \mathcal{W} ({\bf \Lambda}|1+\nu,{\bf W}({\bf x}_*)) \\ ただし {\bf m}({\bf x}_*) &=& \frac{ {\bf x}_* + \beta {\bf m} }{1+\beta} \\ {\bf W}({\bf x}_*)^{-1} &=& \frac{\beta}{1+\beta} ({\bf x}_* - {\bf m})({\bf x}_* - {\bf m})^\mathrm{T} + {\bf W}^{-1} \end{eqnarray} $$
Note: ${\bf W}({\bf x}_*)$の導出。 $$\begin{eqnarray} \\ {\bf W}({\bf x}_*)^{-1} &=& {\bf x}_* {\bf x}_*^\mathrm{T} + \beta {\bf m}{\bf m}^\mathrm{T} - (1+\beta) {\bf m}({\bf x}_*) {\bf m}({\bf x}_*)^\mathrm{T} + {\bf W}^{-1} \\ &=& {\bf x}_* {\bf x}_*^\mathrm{T} + \beta {\bf m}{\bf m}^\mathrm{T} - \frac{1}{1+\beta} ({\bf x}_* + \beta {\bf m}) ({\bf x}_* + \beta {\bf m})^\mathrm{T} + {\bf W}^{-1} \\ &=& (1-\frac{1}{1+\beta}){\bf x}_* {\bf x}_*^\mathrm{T} - \frac{\beta}{1+\beta} {\bf x}_* {\bf m}^\mathrm{T} - \frac{\beta}{1+\beta} {\bf x}_*^\mathrm{T} {\bf m} + (\beta - \frac{\beta^2}{1+\beta}) {\bf m} {\bf m}^\mathrm{T} + {\bf W}^{-1} \\ &=& \frac{\beta}{1+\beta} ({\bf x}_* - {\bf m})({\bf x}_* - {\bf m})^\mathrm{T} + {\bf W}^{-1} \\ \end{eqnarray}$$
これを使って計算する。
$$ \begin{eqnarray} \ln p({\bf x}_*) &=& \ln p({\bf x}_*|{\bf \mu}, {\bf \Lambda}) - \ln p({\bf \mu}, {\bf \Lambda}|{\bf x}_*) + const. \\ &=& \ln \mathcal{N} ({\bf x}_*|{\bf \mu}, {\bf \Lambda}^{-1}) - \ln \mathcal{N}({\bf \mu}|{\bf m}({\bf x}_*), ((1+\beta){\bf \Lambda})^{-1}) - \ln \mathcal{W} ({\bf \Lambda}|1+\nu,{\bf W}({\bf x}_*)) + const. \\ &=& -\frac{1}{2} ({\bf x}_* - {\bf \mu})^\mathrm{T} {\bf \Lambda} ({\bf x}_* - {\bf \mu}) + \frac{1+\beta}{2} ({\bf \mu}-{\bf m}({\bf x}_*))^\mathrm{T} {\bf \Lambda} ({\bf \mu}-{\bf m}({\bf x}_*)) + \frac{1}{2} Tr({\bf W}({\bf x}_*)^{-1} {\bf \Lambda}) + \frac{1+\nu}{2} \ln |{\bf W}({\bf x}_*)| + cosnt. \\ &=& - \frac{1}{2} Tr \left[ \{ ({\bf x}_* - {\bf \mu})({\bf x}_* - {\bf \mu})^\mathrm{T} - (1+\beta) ({\bf \mu}-{\bf m}({\bf x}_*)) ({\bf \mu}-{\bf m}({\bf x}_*))^\mathrm{T} - {\bf W}({\bf x}_*)^{-1} \} {\bf \Lambda} \right] - \frac{1+\nu}{2} \ln |{\bf W}({\bf x}_*)^{-1}| \end{eqnarray} $$トレースの計算。和のトレースはトレースの和であることを利用し、${\bf x}_*$に関わらない部分はconst.にまとめる。
$$ \begin{eqnarray} トレース部分 &=& Tr \left[ \{ ({\bf x}_* - {\bf \mu})({\bf x}_* - {\bf \mu})^\mathrm{T} - (1+\beta) ({\bf \mu}-{\bf m}({\bf x}_*)) ({\bf \mu}-{\bf m}({\bf x}_*))^\mathrm{T} - {\bf W}({\bf x}_*)^{-1} \} {\bf \Lambda} \right] \\ &=& Tr \left[ \{ {\bf x}_* {\bf x}_*^\mathrm{T} - {\bf \mu} {\bf x}_*^\mathrm{T} - {\bf x}_* {\bf \mu}^\mathrm{T} + (1+\beta) {\bf \mu} {\bf m}({\bf x}_*)^\mathrm{T} + (1+\beta) {\bf m}({\bf x}_*) {\bf \mu}^\mathrm{T} - (1+\beta) {\bf m}({\bf x}_*) {\bf m}({\bf x}_*)^\mathrm{T} - \frac{\beta}{1+\beta} {\bf x}_* {\bf x}_*^\mathrm{T} + \frac{\beta}{1+\beta} {\bf m} {\bf x}_*^\mathrm{T} + \frac{\beta}{1+\beta} {\bf x}_* {\bf m}^\mathrm{T} \} {\bf \Lambda} \right] + cosnt. \\ &=& Tr \left[ \{ {\bf x}_* {\bf x}_*^\mathrm{T} - {\bf \mu} {\bf x}_*^\mathrm{T} - {\bf x}_* {\bf \mu}^\mathrm{T} + {\bf \mu} {\bf x}_*^\mathrm{T} + {\bf x}_* {\bf \mu}^\mathrm{T} - \frac{1}{1+\beta}({\bf x}_* + \beta {\bf m})({\bf x}_*^\mathrm{T} + \beta {\bf m}^\mathrm{T}) - \frac{\beta}{1+\beta} {\bf x}_* {\bf x}_*^\mathrm{T} + \frac{\beta}{1+\beta} {\bf m} {\bf x}_*^\mathrm{T} + \frac{\beta}{1+\beta} {\bf x}_* {\bf m}^\mathrm{T} \} {\bf \Lambda} \right] + cosnt. \\ &=& const. \end{eqnarray} $$結局${\bf x}_*$に関わる部分は消えてしまう。
$$ \begin{eqnarray} \ln p({\bf x}_*) &=& - \frac{1+\nu}{2} \ln |{\bf W}({\bf x}_*)^{-1}| + const. \\ &=& - \frac{1+\nu}{2} \ln |\frac{\beta}{1+\beta} ({\bf x}_* - {\bf m})({\bf x}_* - {\bf m})^\mathrm{T} + {\bf W}^{-1}| + const. \\ &=& - \frac{1+\nu}{2} \ln \{ 1 + \frac{\beta}{1+\beta} ({\bf x}_* - {\bf m})^\mathrm{T} {\bf W} ({\bf x}_* - {\bf m}) \} + const. (精度未知の時と同様に式変形を行った。) \end{eqnarray} $$これは多次元のStudentのt分布の対数表現である。対応をとって
$$ \begin{eqnarray} p({\bf x}_*) &=& St({\bf x}_* | {\bf \mu}_s, {\bf \Lambda}_s, \nu_s) \\ ただし {\bf \mu}_s &=& {\bf m} \\ {\bf \Lambda}_s &=& \frac{(1-D+\nu)\beta}{1+\beta} {\bf W} \\ \nu_s &=& 1 - D + \nu \end{eqnarray} $$となる。学習後の予測分布は更新されたハイパーパラメータを代入することで求まる。
Juliaによる実装
平均未知・精度行列未知の場合のみ実装します。
D=2, N=100とします。
# 乱数生成のためのパッケージ
using Random
# 行列計算用のパッケージ
using LinearAlgebra
# グラフ描画用のパッケージ
ENV["GKS_ENCODING"]="utf8" # Plot内でunicode使うためのおまじない
using Plots
using Plots.PlotMeasures
using StatsPlots
# 確率分布の関数を呼び出すパッケージ
using Distributions
# 真の分布のパラメータ
mu_true = [5., 10.]
Sigma_true = [5. 0.5;0.5 5.]
Lambda_true = inv(Sigma_true)
# 0~100までの数列
Ns = 0:100;
# 100個のデータ
Random.seed!(12)
data = rand(MvNormal(mu_true, Sigma_true), last(Ns))
# 最初の5個
data[:, 1:5]
data[:,1:100] * data[:,1:100]'
#hide_output
D=2
# 事前分布のハイパーパラメータ
m = [1., 1.]
beta = 1.
nu = 2. # >D-1である
W = [1. 0. ;0. 1.]
# ベイズ推論の進行過程をアニメーションに
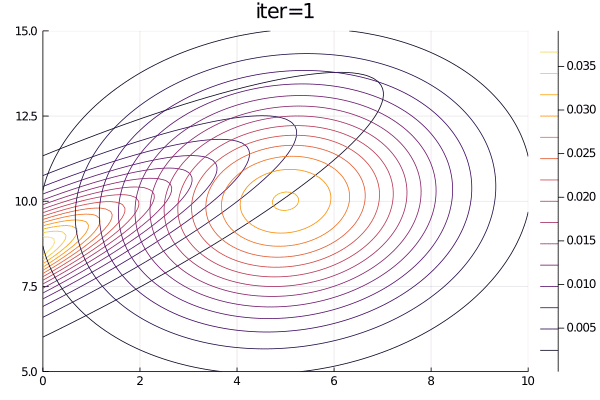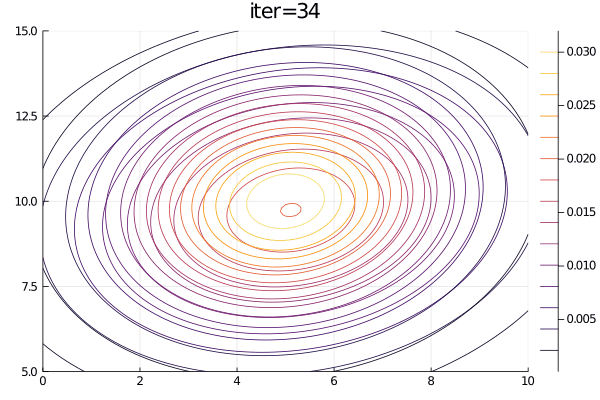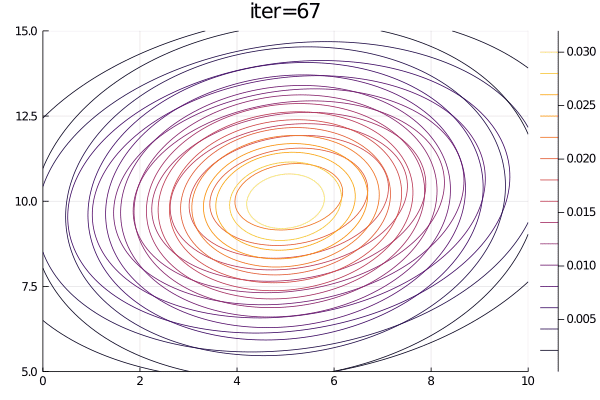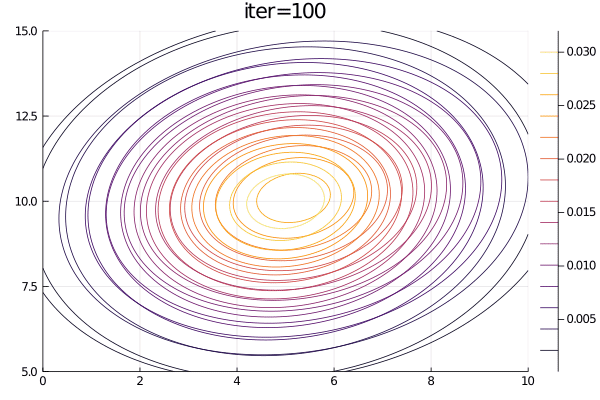
animation = @animate for i = 1:100
# ハイパーパラメータを更新
beta_hat = i + beta
m_hat = vec((sum(data[:, 1:i], dims=2) .+ beta .* m) ./ beta_hat)
nu_hat = i + nu
Sigma_xn_xn = sum([data[:,j]*data[:,j]' for j = 1:i])
W_hat = Matrix(Hermitian(inv(Sigma_xn_xn .+ beta .* (m * m') .- beta_hat .* (m_hat * m_hat') .+ inv(W))))
# 事後確率分布
updated_Wishart = Wishart(nu_hat, W_hat)
updated_Normal = MvNormal(m_hat, beta_hat .* Matrix(Hermitian(inv(rand(updated_Wishart)))))
# 予測分布のパラメータ
mu_s = m_hat
Lambda_s = ((1-D+nu_hat)*beta_hat/(1+beta_hat)) .* W_hat
nu_s = 1 - D + nu_hat
# 予測分布
predict = MvTDist(nu_s, mu_s, inv(Lambda_s))
# 描画用の関数
x1 = 0. :0.1: 10.
x2 = 5. :0.1: 15.
# 平均の事後分布 コードだけ
# pdf_post(x, y) = pdf(updated_Normal, [x, y])
# pdf_post.(x1,x2') == [pdf_post(x, y) for x in x1, y in x2 ]
# p1 = contour(x1,x2,pdf_post.(x1,x2'))
# 予測分布
pdf_predict(x, y) = pdf(predict, [x, y])
pdf_predict.(x1,x2') == [pdf_predict(x, y) for x in x1, y in x2]
p2 = contour(x1,x2,pdf_predict.(x1,x2'))
# 真の分布
pdf_true(x, y) = pdf(MvNormal(mu_true, Sigma_true), [x, y])
pdf_true.(x1,x2') == [pdf_true(x, y) for x in x1, y in x2]
contour!(p2, x1,x2,pdf_true.(x1,x2'))
plot(p2, title="iter=$i")
end;
gif(animation, "animations/mgauss_ml.gif", fps = 15)
