ベイズ勉強会資料は『ベイズ推論による機械学習入門』1を元に、途中式計算をできるだけ省略せずに行ったものです。

概論: ベイズ推論のワークフロー

Important: ベイズ推論の共通するワークフロー
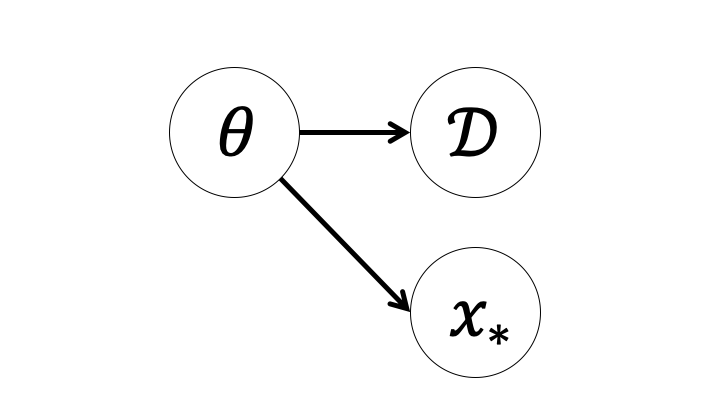
  1. 観測データ$\mathcal{D}$と観測されていない未知の変数$\mathbf{X}$の同時分布$p(\mathcal{D}, \mathbf{X})$を構築
  2. 事後分布$p(\mathbf{X}|\mathcal{D}) = \frac{p(\mathcal{D}, \mathbf{X})}{p(\mathcal{D})}$を求める。

今回はさらに事後分布を用いて予測分布を計算するところまでを見る。

予測分布

観測されたデータ$\mathcal{D}$に対して、パラメタ$\theta$を持つ確率分布でモデルを組み、新しいデータ$x_*$を予測したい。$\mathcal{D}$と$x_*$が独立に生成されるとすると、以下のような予測分布を用いることができる。

$$p(x_*|\mathcal{D}) = \int p(x_*|\theta)p(\theta|\mathcal{D}) d\theta$$

$\mathcal{D}$, $\theta$, $x_*$の関係をDAGで表すと次のようになる。

この時、$\mathcal{D}$と$x_*$はパラメタ$\theta$が与えられた条件の下での条件付き独立である。

同時分布の記述

$\mathcal{D}$と$x_*$がパラメタ$\theta$が与えられた条件の下での条件付き独立であることから同時分布は以下のようになる。 $$ p(\mathcal{D}, x_*, \theta) = p(\mathcal{D}|\theta)p(x_*|\theta)p(\theta) $$

Note: $p(\theta)$は2個必要なのではないかと思うかもしれない。サイコロの目によって動きが決まる駒が2つあり、同時に動かす状況を考えよう。コマの動きを決めるのにサイコロを振る回数は1回である。

Note: $p(\mathcal{D}|\theta)$の部分はパラメタからデータが生成される過程を記述している。これを$\theta$の関数として見た場合尤度関数と呼ぶ。この尤度関数を最大化する$\theta$を$\theta$の予測値とする方法を最尤推定という。

Note: $p(\theta)$を事前分布という。同時確率は尤度関数×事前分布の形で書くことができる。

事後分布の推論

データ$\mathcal{D}$だけが手元にある時、残りの変数の事後分布は $$ \begin{eqnarray} p(x_*, \theta|\mathcal{D}) &=& \frac{p(\mathcal{D}, x_*, \theta)}{p(\mathcal{D})} \\ &=& \frac{p(\mathcal{D}|\theta)p(x_*|\theta)p(\theta)}{p(\mathcal{D})} \\ &=& p(x_*|\theta)p(\theta|\mathcal{D}) \end{eqnarray} $$ となる。

Note: ベイズの定理から$p(\theta|\mathcal{D}) = \frac{p(\mathcal{D}|\theta)p(\theta)}{p(\mathcal{D})}$となることを用いた。

Note: $p(\theta|\mathcal{D})$を最大化する$\theta$を$\theta$の予測値とする方法を事後確率最大化推定(MAP推定)と呼ぶ。

予測分布の算出

$\mathcal{D}$が決まった時の$x_*$の確率分布、すなわち予測分布$p(x_*|\mathcal{D})$は$\theta$を積分除去することで得られる。

$$p(x_*|\mathcal{D}) = \int p(x_*|\theta)p(\theta|\mathcal{D}) d\theta$$

以上がベイズ推論の予測までを含めた一連の流れである。次回から離散確率分布について具体的にやってみる。

1. 須山敦志. 杉山将. ベイズ推論による機械学習入門. 講談社, 2017.↩